A Brief Introduction to Reinforcement Learning for All

2024 Turing Award to Reinforcement Learning

https://yuxili.substack.com/p/2024-turing-award-to-reinforcement

Here is a brief introduction to reinforcement learning (RL) for all.

The outline follows:

1. RL vs Machine Learning vs Deep Learning vs AI

2. A Brief Introduction to RL

3. A Shortest Path Example

4. RL vs Intelligence

5. RL vs Optimal Control and Operations Research

6. Opportunities

7. Challenges

8. When is RL helpful?

9. Why has RL not been widely adopted in practice yet?

RL vs Machine Learning vs Deep Learning vs AI

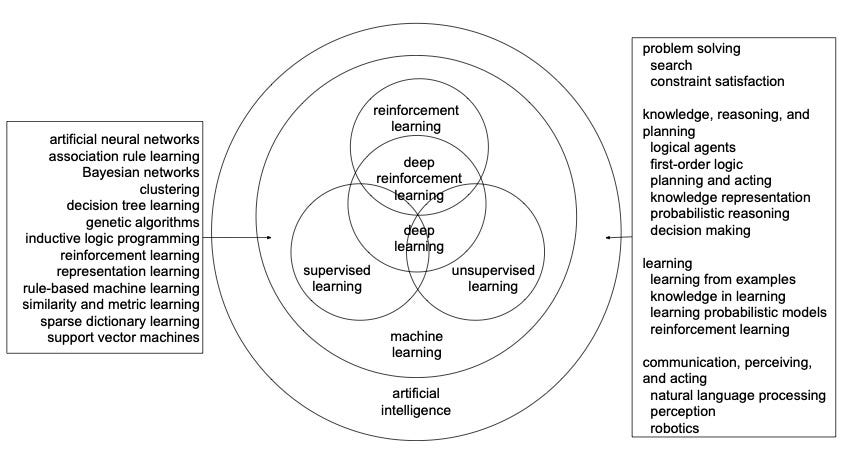
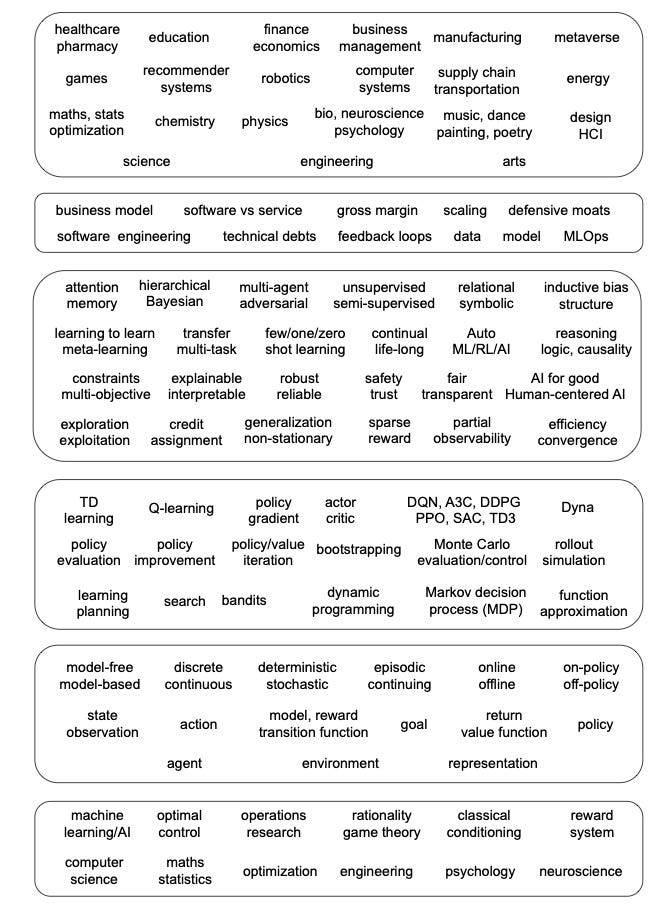
Machine learning is about learning from data and making predictions and/or decisions. We usually categorize machine learning into supervised learning, unsupervised learning, and reinforcement learning (RL). Supervised learning works with labeled data, including classification and regression with categorical and numerical outputs, respectively. Unsupervised learning finds patterns from unlabelled data, e.g., clustering, principle component analysis (PCA) and generative adversarial networks (GANs). In RL, there are evaluative feedbacks but no supervised labels. Evaluative feedbacks can not indicate whether a decision is correct or not, as labels in supervised learning. Supervised learning is usually one-step, and considers only immediate cost or reward, whereas RL is sequential, and ideal RL agents are far-sighted and consider long-term accumulative rewards. RL has additional challenges like credit assignment and exploration vs. exploitation, comparing with supervised learning. Moreover, in RL, an action can affect next and future states and actions, which results in distribution shift inherently. Deep learning (DL), or deep neural networks (DNNs), can work with/as these and other machine learning approaches. Deep learning is part of machine learning, which is part of AI. Deep RL is an integration of deep learning and RL.The following figure presents the relationship among these concepts.

Relationship among reinforcement learning, deep learning, deep reinforcement learn- ing, supervised learning, unsupervised learning, machine learning, and AI. Deep reinforcement learning, as the name indicates, is at the intersection of deep learning and reinforcement learning. We usually categorize machine learning as supervised learning, unsupervised learning, and reinforcement learning. However, they may overlap with each other. Deep learning can work with/as these and other machine learning approaches. Deep learning is part of machine learning, which is part of AI. The approaches in machine learning on the left is based on Wikipedia, https://en.wikipedia.org/wiki/Machine_learning. The approaches in AI on the right is based on Russell and Norvig (2009). Note that all these fields are evolving, e.g., deep learn- ing and reinforcement learning are addressing many classical AI problems, such as logic, reasoning, and knowledge representation.

A Brief Introduction to RL

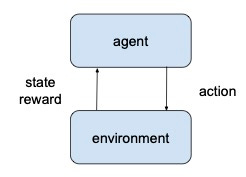
An RL agent interacts with the environment over time to learn a policy, by trial and error, that maximizes the long-term, cumulated reward. At each time step, the agent receives an observation, selects an action to be executed in the environment, following a policy, which is the agent’s behaviour, i.e., a mapping from an observation to actions. The environment responds with a scalar reward and by transitioning to a new state according to the environment dynamics. The following figure illustrates the agent-environment interaction.

In an episodic environment, this process continues until the agent reaches a terminal state and then it restarts. Otherwise, the environment is continuing without a terminal state. There is a discount factor to measure the influence of future award. The model refers to the transition probability and the reward function. The RL formulation is very general: state and action spaces can be discrete or continuous; an environment can be a multi-armed bandit, an MDP, a partially observable MDP (POMDP), a game, etc.; and an RL problem can be deterministic, stochastic, dynamic, or adversarial.

A state or action value function measures the goodness of each state or state action pair, respectively. It is a prediction of the return, or the expected, accumulative, discounted, future reward. The action value function is usually called the Q function. An optimal value is the best value achievable by any policy, and the corresponding policy is an optimal policy. An optimal value function encodes global optimal information, i.e., it is not hard to find an optimal policy based on an optimal state value function, and it is straightforward to find an optimal policy with an optimal action value function. The agent aims to maximize the expectation of a long-term return or to find an optimal policy.

When the system model is available, we may use dynamic programming methods: policy evaluation to calculate value/action value function for a policy, and value iteration or policy iteration for finding an optimal policy, where policy iteration consists of policy evaluation and policy improvement. Monte Carlo (MC) methods learn from complete episodes of experience, not assuming knowledge of transition nor reward models, and use sample means for estimation. Monte Carlo methods are applicable only to episodic tasks. In model-free methods, the agent learns with trail and error from experience directly; the model, usually the state transition, is not known. RL methods that use models are model-based methods; the model may be given or learned from experience.

The prediction problem, or policy evaluation, is to compute the state or action value function for a policy. The control problem is to find the optimal policy. Planning constructs a value function or a policy with a model.

In an online mode, an algorithm is trained on data available in sequence. In an offline mode, or a batch mode, an algorithm is trained on a collection of data.

Temporal difference (TD) learning learns state value function directly from experience, with boot-strapping from its own estimation, in a model-free, online, and fully incremental way. With boot-strapping, an estimate of state or action value is updated from subsequent estimates. TD learning is an on-policy method, with samples from the same target policy. Q-learning is a temporal difference control method, learning an optimal action value function to find an optimal policy. Q-learning is an off-policy method, learning with experience trajectories from some behaviour policy, but not necessarily from the target policy. The notion of on-policy and off-policy can be understood as “same-policy” and “different-policy”, respectively.

In tabular cases, a value function and a policy are stored in tabular forms. Function approximation is a way for generalization when the state and/or action spaces are large or continuous. Function approximation aims to generalize from examples of a function to construct an approximate of the entire function. Linear function approximation is a popular choice, partially due to its desirable theoretical properties. A function is approximated by a linear combination of basis functions, which usually need to be designed manually. The coefficients, or weights, in the linear combination, need to be found by learning algorithms.

We may also have non-linear function approximation, in particular, with DNNs, to represent the state or observation and/or actions, to approximate value function, policy, and model (state transition function and reward function), etc. Here, the weights in DNNs need to be found. We obtain deep RL methods when we integrate deep learning with RL. Deep RL is popular and has achieved stunning achievements recently.

TD learning and Q-learning are value-based methods. In contrast, policy-based methods optimize the policy directly, e.g., policy gradient. Actor-critic algorithms update both the value function and the policy.

There are several popular deep RL algorithms. DQN integrates Q-learning with DNNs, and utilizes the experience replay and a target network to stabilize the learning. In experience replay, experience or observation sequences, i.e., sequences of state, action, reward, and next state, are stored in the replay buffer, and sampled randomly for training. A target network keeps its separate network parameters, which are for the training, and updates them only periodically, rather than for every training iteration. Mnih et al. (2016) present Asynchronous Advantage Actor-Critic (A3C), in which parallel actors employ different exploration policies to stabilize training, and the experience replay is not utilized. Deterministic policy gradient can help estimate policy gradients more efficiently. Silver et al. (2014) present Deterministic Policy Gradient (DPG) and Lillicrap et al. (2016) extend it to Deep DPG (DDPG). Trust region methods are an approach to stabilize policy optimization by constraining gradient updates. Schulman et al. (2015) present Trust Region Policy Optimization (TRPO) and Schulman et al. (2017) present Proximal Policy Optimization (PPO). Haarnoja et al. (2018) present Soft Actor-Critic (SAC), an off-policy algorithm aiming to simultaneously succeed at the task and act as randomly as possible. Fujimoto et al. (2018) present Twin Delayed Deep Deterministic policy gradient algorithm (TD3) to minimize the effects of overestimation on both the actor and the critic. Fujimoto and Gu (2021) present a variant of TD3 for offline RL.

A fundamental dilemma in RL is the exploration vs. exploitation tradeoff. The agent needs to exploit the currently best action to maximize rewards greedily, yet it has to explore the environment to find better actions, when the policy is not optimal yet, or the system is non-stationary. A simple exploration approach is ε-greedy, in which an agent selects a greedy action with probability 1 − ε, and a random action otherwise.

A Shortest Path Example

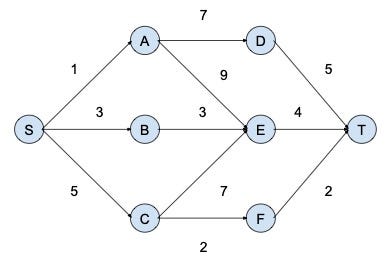
Consider the shortest path problem as an example. The single-source shortest path problem is to find the shortest path between a pair of nodes to minimize the distance of the path, or the sum of weights of edges in the path. We can formulate the shortest path problem as an RL problem. The state is the current node. At each node, following the link to each neighbour is an action. The transition model indicates that the agent goes to a neighbour after choosing a link to follow. The reward is then the negative of link cost. The discount factor can be 1, so that we do not differentiate immediate reward and future reward. It is fine since it is an episodic problem. The goal is to find a path to maximize the negative of the total cost, i.e., to minimize the total distance. An optimal policy is to choose the best neighbour to traverse to achieve the shortest path; and, for each state/node, an optimal value is the negative of the shortest distance from that node to the destination.

An example is shown in the following figure, with the graph nodes, (directed) links, and costs on links. We want to find the shortest path from node S to node T. We can see that if we choose the nearest neighbour of node S, i.e., node A, as the next node to traverse, then we cannot find the shortest path, i.e., S → C → F → T . This shows that a short-sighted choice, e.g., choosing node A to traverse from node S, may lead to a sub-optimal solution. RL methods, like TD-learning and Q-learning, can find the optimal solution by considering long-term rewards.

Some readers may ask why not use Dijkstra’s algorithm. Dijkstra’s algorithm is an efficient algo- rithm, with the global information of the graph, including nodes, edges, and weights. RL can work without such global graph information by wandering in the graph according to some policy, i.e., in a model-free approach. With such graph information, Dijkstra’s algorithm is efficient for the particular shortest path problem. However, RL is more general than Dijkstra’s algorithm, applicable to many problems, e.g., a problem with stochastic weights or a new instance with meta-learning.

RL vs Intelligence

Reinforcement Learning (RL) is rooted in optimal control (in particular, dynamic programming and Markov decision process), learning by trail and error, and temporal difference learning, the latter two being related to animal learning. RL has foundation in theoretical computer science/machine learning, classical AI, optimization, statistics, optimal control, operations research, neuroscience, and psychology. (At the same time, RL also influences these disciplines.) RL has both art and science components. Rather than making it pure science, we need to accept that part of it is art.

The following are literal quotes from Section 1.6 in Sutton and Barto (2018). “Reinforcement learning is a computational approach to understanding and automating goal-directed learning and decision making. It is distinguished from other computational approaches by its emphasis on learning by an agent from direct interaction with its environment, without requiring exemplary supervision or complete models of the environment. In our opinion, reinforcement learning is the first field to seriously address the computational issues that arise when learning from interaction with an environment in order to achieve long-term goals.” “Reinforcement learning uses the formal framework of Markov decision processes to define the interaction between a learning agent and its environment in terms of states, actions, and rewards. This framework is intended to be a simple way of representing essential features of the artificial intelligence problem. These features include a sense of cause and effect, a sense of uncertainty and nondeterminism, and the existence of explicit goals.”

Sutton (2022) proposes the common model of the intelligent agent for decision making across psychology, artificial intelligence, economics, control theory, and neuroscience, with the terminology of agent, world, observation, action and reward.

Richard Sutton discusses briefly about David Marr’s three levels at which any information process- ing machine must be understood: computational theory, representation and algorithm, and hardware implementation.10 AI has surprisingly little computational theory. The big ideas are mostly at the middle level of representation and algorithm. RL is the first computational theory of intelligence. RL is explicitly about the goal, the whats and whys of intelligence.

RL is a set of sequential decision problems. It is not a specific set of algorithmic solutions, like TD, DQN, PPO, evolutionary search, random search, semi-supervised learning, etc. RL has three basic problems and many variations: online RL, offline / batch RL, and planning/simulation optimization. See Szepesvari (2020c).

RL methods deal with sampled, evaluative and sequential feedback, three weak forms of feedback simultaneously, compared with exhaustive, supervised and one-shot feedback (Littman, 2015).

RL vs Optimal Control and Operations Research

Traditionally optimal control (OC) and operations research (OR) require a perfect model for the problem formulation. RL can work in a model-free mode, and can handle very complex problems via simulation, which may be intractable for model-based OC or OR approaches. AlphaGo, together with many games, are huge problems. RL with a perfect model can return a perfect solution, in the limit. RL with a decent simulator or with decently sufficient amount of data can provide a decent solution. Admittedly, there are adaptive and/or approximate approaches in OC and OR working with imperfect models, and/or for large-scale problems. We see that RL, optimal control, and operations research are merging and advancing together, which is beneficial and fruitful for all these scientific communities.

Sutton and Barto (2018) discuss the relationship between RL and optimal control in Section 1.7, where we quote the following verbatim. “We consider all of the work in optimal control also to be, in a sense, work in reinforcement learning. We define a reinforcement learning method as any effective way of solving reinforcement learning problems, and it is now clear that these problems are closely related to optimal control problems, particularly stochastic optimal control problems such as those formulated as MDPs. Accordingly, we must consider the solution methods of optimal control, such as dynamic programming, also to be reinforcement learning methods. Because almost all of the conventional methods require complete knowledge of the system to be controlled, it feels a little unnatural to say that they are part of reinforcement learning. On the other hand, many dynamic programming algorithms are incremental and iterative. Like learning methods, they gradually reach the correct answer through successive approximations. As we show in the rest of this book, these similarities are far more than superficial. The theories and solution methods for the cases of complete and incomplete knowledge are so closely related that we feel they must be considered together as part of the same subject matter.”

Bertsekas (2019a;b) presents ten key ideas for RL and optimal control: 1) principle of optimality, 2) approximation in value space, 3) approximation in policy space, 4) model-free methods and simulation, 5) policy improvement, rollout, and self-learning 6) approximate policy improvement, adaptive simulation, and Q-learning, 7) features, approximation architectures, and deep neural nets, 8) incremental and stochastic gradient optimization, 9) direct policy optimization: a more general approach, and 10) gradient and random search methods for direct policy optimization.

Powell (2019) regards RL as sequential decision problems, and identifies four types of policies: 1) policy function approximations, e.g., parameterized policies, 2) cost function approximations, e.g., upper confidence bounding (UCB), 3) value function approximations, e.g., Q-learning, and 4) direct lookahead, e.g., Monte Carlo tree search (MCTS), claiming they are universal, i.e., “any policy proposed for any sequential decision problem will consist of one of these four classes, and possibly a hybrid”. Powell (2019) proposes a unified framework based on stochastic control.

Szepesva ́ri (2020c) discusses that RL is not the answer to everything and RL is not the set of popular methods like TD, DQN and PPO. It is normal for certain methods like model predictive control (MPC) and random search to perform well on certain tasks. Methods have strengths and weaknesses. For a certain task, besides RL, we should consider other methods.

Bertsekas (2022) discusses lessons from AlphaZero for continuous problems in optimal, model predictive, and adaptive control. Levine (2018) regards RL and control as probabilistic inference. Recht (2019) surveys RL from the perspective of optimization and control.

There are several recent books at the intersection of RL and optimal control and/or operations research, e.g. Bertsekas (2019a); Powell (2021); Meyn (2022).

Opportunities

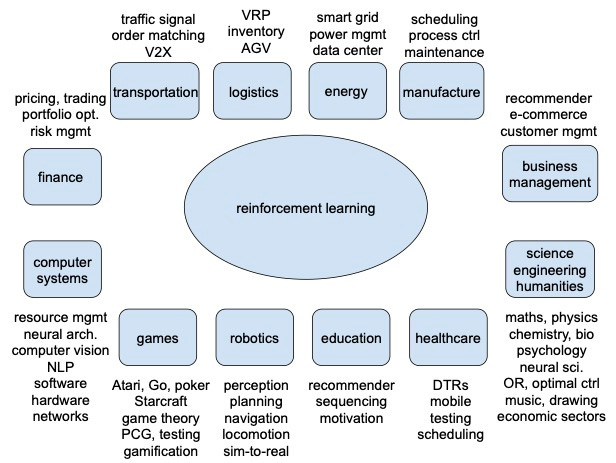
Some years ago we talked about potential applications of machine learning in industry, and machine learning is already in many large scale production systems. Now we are talking about RL, and RL starts to appear in production systems. Contextual bandits are a “mature” technique that can be widely applied. RL is “mature” for many single-, two-, and multi-player games. We will proba- bly see more results in recommendation/personalization soon. System optimization and operations research are expected to draw more attention. Robotics and healthcare are already at the center of attention. In the following, we discuss several successful applications. Note, topics in subsections may overlap, e.g, robotics may also appear in education and healthcare, computer systems are involved in all topics, combinatorial optimization can be applied widely, like in transportation and computer systems, and science and engineering are general areas. There are vast number of papers about RL applications. See e.g., Li (2019b) and a blog. (Both were last updated in 2019.)

Challenges

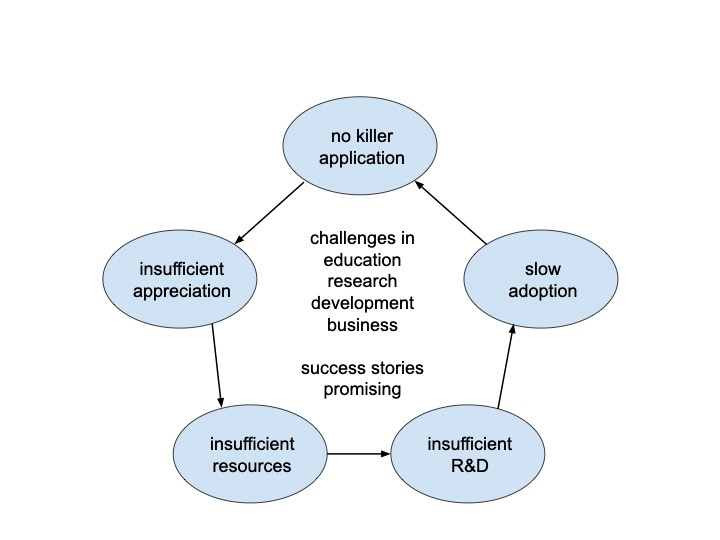
Although RL has made significant progress, there are still many issues. Sample efficiency, credit assignment, exploration vs. exploitation, and representation are common issues. Value function approaches with function approximation, in particular with DNNs, encounters the deadly triad, i.e., instability and/or divergence caused by the integration of off-policy, function approximation, and bootstrapping. Reproducibility is an issue for deep RL, i.e., experimental results are influenced by hyperparameters, including network architecture and reward scale, random seeds and trials, environments, and codebases (Henderson et al., 2018). Reward specification may cause problems, and a reward function may not represent the intention of the designer. Researchers and practitioners are still identifying issues, e.g., delusional bias (Lu et al., 2018) and expressivity of Markov reward (Abel et al., 2021), and address them. The following figure illustrates challenges of reinforcement learning.

Dulac-Arnold et al. (2021) identify nine challenges for RL to be deployed in real-life scenarios, namely, learning on the real system from limited samples, system delays, high-dimensional state and action spaces, satisfying environmental constraints, partial observability and non-stationarity, multi-objective or poorly specified reward functions, real-time inference, offline RL training from fixed logs, and explainable and interpretable policies. Practitioners report lessons in RL deployment, e.g., Rome et al. (2021), Karampatziakis et al. (2019).

Bearing in mind that there are many issues, there are efforts to address all of them, and RL is an effective technique for many applications. As discussed by Dimitri Bertsekas, on one hand, there are no methods that are guaranteed to work for all or even most problems; on the other hand, there are enough methods to try with a reasonable chance of success for most types of optimization prob- lems: deterministic, stochastic, or dynamic ones, discrete or continuous ones, games, etc. (Bertsekas, 2019b)

When is RL helpful?

In general, RL can be helpful, if a problem can be regarded as or transformed to a sequential decision making problem, and states/observations, actions, and (sometimes) rewards can be constructed. RL is helpful for goal-directed learning. RL may help to automate and optimize previously manually designed strategies. The rate of success expects to be higher if a problem comes with a perfect model, a high-fidelity simulator, or a large amount of data.

For the current state of the art, RL is helpful when big data are available, from a model, from a good simulator/digital twin, or from interactions (online or offline). For a problem in natural science and engineering, the objective function may be clear, with a standard answer, and straightforward to evaluate. For example, AlphaGo has a perfect simulator and the objective is clear, i.e., to win. Good models/simulators usually come with many problems in combinatorial optimization, operations re- search, optimal control, drug design, etc. (Admittedly, there may be multiple objectives or reward is non-trivial to specify.) In contrast, for a problem in social science and arts, usually there are people involved, thus the problem is influenced by psychology, behavioural science, etc., the objective is usually subjective, may not have a standard answer, and may not be easy to evaluate. Example appli- cations include education and game design. Recommender systems usually have bountiful data, so there are successful production systems. However, there are still challenges for those facing human users. Recent progress in RL from human feedback has shown its benefits in human value alignment. Concepts like psychology, e.g. intrinsic motivation, flow and self-determination theory, may serve as a bridge connecting RL/AI with social science and arts, e.g., by defining a reward function.

Why has RL not been widely adopted in practice yet?

The big chicken-egg loop: no killer application, insufficient appreciation from higher management, insufficient resources, insufficient R&D, slow adoption, then, as a result, non-trivial to have a killer application. There are underlying challenges from education, research, development and business. The status quo is actually much better, having many success stories. With challenges, RL is promising.

Notes

+ This blog is basically excerpts from Reinforcement Learning in Practice: Opportunities and Challenges https://arxiv.org/abs/2202.11296 (Feb 2022)

+ See reference in it.

+ It contains the following, about RLHF:

Christiano et al. (2017) propose the approach of RL from human feedback, i.e., by defining a reward function with preferences between pairs of trajectory segments, to tackle the problems without well-defined goals and without experts’ demonstrations, and to help improve the alignment between humans’ values and the objectives of RL systems. Lee et al. (2021a) present unsupervised pre-training and preference-based learning via relabeling experience, to improve the efficiency of human-in-the-loop feedbacks with binary labels, i.e. preferences, provided by a supervisor. Ouyang et al. (2022) propose to fine-tune large language models GPT-3 with human feedback, in particular, with RL (Christiano et al., 2017), to follow instructions for better alignment with humans’ values. Wirth et al. (2017) present a survey of preference-based RL methods. Zhang et al. (2021b) survey human guidance for sequential decision-making.

+ This blog does not cover RL for LLMs.

+ Csaba Szepesvári, Myths and Misconceptions in RL, https://sites.ualberta.ca/~szepesva/talks.html

+ Rich Sutton, A Perspective on Intelligence,

+ David Silver, David Silver - Towards Superhuman Intelligence,